Maximum Weighted Independent Set

The maximum independent set problem is one of the fundamental problems in combinatorial optimization with ubiquitous applications and connections to other problems. Maximum clique, minimum vertex cover, and maximum matching are a few examples of problems that can be reduced to a maximum independent set problem.

In this Mod, we consider the more general problem of the maximum weighted independent set (MWIS), which has applications in various fields such as computer vision, pattern recognition, molecular structure matching, social network analysis, and genome data mapping. To better understand how a theoretical graph theory problem can be used to address a real-world challenge, let us review one application area in detail.

To measure the structural similarity between two molecules, the molecules are first represented as labeled graphs where the vertices and the edges correspond to the atoms of the molecule and its chemical bonds, respectively. To find the largest substructure (subgraph) that appears in both molecular graphs, it suffices to find the maximum weighted independent set of a third graph, known as conflict graph. The vertices and the edges of the conflict graph represent possible mappings and conflicts between two molecules, respectively.

Problem Specification

Consider an undirected graph \(G\) with \(n\) vertices and \(m\) edges where each vertex is associated with a positive weight \(w\). Find a maximum weighted independent set, i.e., select a set of vertices in graph \(G\) where there is no edge between any pair of selected vertices and the sum of the vertex weights for this set is maximised.

More formally stated, let \(G = (V, E, w)\) be an undirected graph where each vertex \(i \in V\) has a positive weight \(w_i\). Find a subset \(S \subseteq V\) such that:

  • no two vertices in \(S\) are connected by an edge; and

  • among all such independent sets, the set \(S\) has the maximum total vertex weight.

Background: Optimization Model

This Mod is implemented by formulating a Binary Integer Programming (BIP) model and solving it using Gurobi. For each vertex \(i \in V\), define a binary decision variable \(x_i\) as below:

\[\begin{split}x_i = \begin{cases} 1 & \text{if vertex}\,i\,\text{belongs to set}\,S\,\\ 0 & \text{otherwise.} \\ \end{cases}\end{split}\]

The formulation of the MWIS is then given below:

\[\begin{split}\begin{align} \max \quad & \sum_{i \in V} w_i x_i \\ \mbox{s.t.} \quad & x_i + x_j \leq 1 & \forall (i, j) \in E \\ & x_i \in \{0, 1\} & \forall i \in V \end{align}\end{split}\]

The input data for this Mod includes a scipy sparse matrix in CSR (Compressed SparseRow) format that captures the adjacency matrix of the graph \(G\) (upper triangle only), plus a numpy array that captures the weights of the vertices.

Code

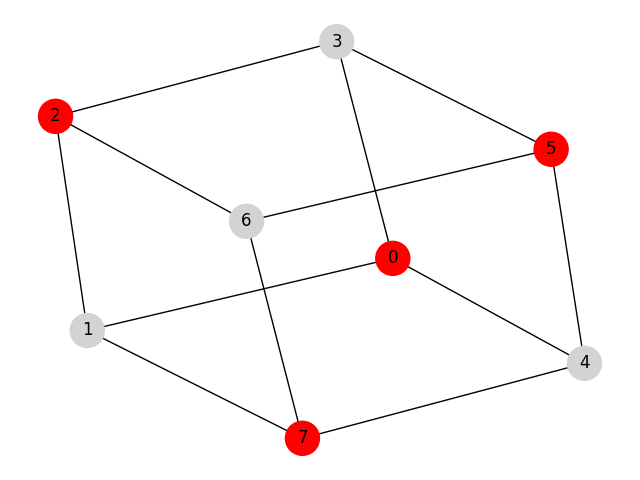
The example below finds a maximum weighted independent set for a graph with 8 vertices and 12 edges known as the cube graph.

import scipy.sparse as sp
import networkx as nx
import numpy as np
from gurobi_optimods.mwis import maximum_weighted_independent_set

# Graph adjacency matrix (upper triangular) as a sparse matrix.
g = nx.cubical_graph()
adjacency_matrix = sp.triu(nx.to_scipy_sparse_array(g))
# Vertex weights
weights = np.array([2**i for i in range(8)])

# Compute maximum weighted independent set.
mwis = maximum_weighted_independent_set(adjacency_matrix, weights)

Solution

The solution is a numpy array containing the vertices in set \(S\).

>>> mwis
array([0, 2, 5, 7])
>>> maximum_vertex_weight = sum(weights[mwis])
>>> maximum_vertex_weight
165

>>> import networkx as nx
>>> import matplotlib.pyplot as plt
>>> layout = nx.spring_layout(g, seed=0)
>>> color_map = ["red" if node in mwis else "lightgrey" for node in g.nodes()]
>>> nx.draw(g, pos=layout, node_color=color_map, node_size=600, with_labels=True)

The vertices in the independent set are highlighted in red.

../_images/mwis.png