Maximum Bipartite Matching
The maximum matching problem is a fundamental problem in graph theory. Given a graph, as a set of nodes connected to one another by edges, a matching is any subset of those edges which have no vertex in common. The goal of maximum matching is to find the largest possible such matching of a given graph.
In this mod we consider the special case of maximum cardinality matching on bipartite graphs. This problem can be applied to solve exclusive assignment problems in practice, such as the assignment of workers or resources to tasks. To give a brief example, if we construct a bipartite graph where one of the bipartite sets represents tasks, and the other workers, then a matching is a set of edges each of which assigns one worker to one task. By the properties of a matching, each worker is assigned at most one task and each task is completed by at most one worker. The maximum cardinality matching is one which maximises the number of completed tasks (and workers given work).

A bipartite graph (left) and its maximum matching (right)
Problem Specification
Consider a bipartite graph \(G(U, V, E)\), where \(U\) and \(V\) are disjoint vertex sets, and the edge set \(E \subseteq U \times V\) joins only between, not within, the sets. A matching on this graph is any subset of edges such that no vertex is incident to more than one edge. Equivalently, the matching is a subgraph of \(G\) where all vertices have degree at most one. A maximum matching is the largest possible matching on \(G\).
Background: Mathematical Model
The bipartite matching Mod is implemented by reducing the basic version of the problem to a minimum-cost flow problem. To do so, we introduce a source vertex as a predecessor to all vertices in \(U\), and a sink vertex as a successor to all vertices in \(V\). Giving every edge unit capacity, a maximum matching is found by maximizing flow from the source to the sink. As a min-cost flow, this is equivalent to adding an edge with a negative cost from the sink to the source and assigning zero cost to all other edges. All edges with non-zero flow in the min-cost flow solution are part of the matching.
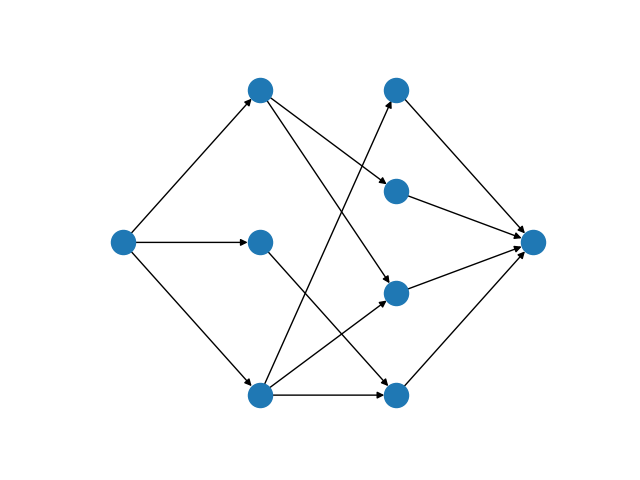
A maximum flow network for the bipartite matching problem
We do not describe the mathematical formulation here, see Minimum-Cost Flow for details. The important point to note is that when this continuous model is solved using the simplex algorithm, we are guaranteed to get an integral solution and thus the solution can be used to select a set of edges for the matching.
Interface
The maximum_bipartite_matching function supports scipy sparse arrays, pandas
dataframes, and networkx graphs as possible inputs. The user must also provide
the bipartite partitioning of the input graph. In all cases, the matching is
returned as a sub-graph of the input data structure.
When given a scipy sparse array representing the adjacency matrix of the graph, the user must also provide the two disjoint node sets as numpy arrays. The mod will return the adjacency matrix of the matching as a scipy sparse array.
import numpy as np
import scipy.sparse as sp
from gurobi_optimods.bipartite_matching import maximum_bipartite_matching
# Create a simple bipartite graph as a sparse matrix
nodes1 = np.array([0, 1, 2, 3, 4])
nodes2 = np.array([5, 6, 7])
row = [0, 3, 4, 0, 1, 3]
col = [7, 5, 5, 6, 6, 7]
data = [1, 1, 1, 1, 1, 1]
adjacency = sp.coo_array((data, (row, col)), shape=(8, 8))
# Compute the maximum matching
matching = maximum_bipartite_matching(adjacency, nodes1, nodes2)
When given a networkx graph as input, the user must also provide the two disjoint node sets as numpy arrays. The mod will return the matching as a networkx graph (a subgraph of the input).
import networkx as nx
import numpy as np
from gurobi_optimods.bipartite_matching import maximum_bipartite_matching
# Create a random bipartite graph
graph = nx.bipartite.random_graph(n=5, m=4, p=0.4, seed=123)
nodes1 = np.arange(5)
nodes2 = np.arange(5, 5 + 4)
# Compute the maximum matching
matching = maximum_bipartite_matching(graph, nodes1, nodes2)
The mod accepts pandas dataframes as input, where two columns in the dataframe describe the source and target vertices of an edge. The user must also provide the source and target column names as inputs to the mode. The matching will be returned as a subset of the rows in the original dataframe, including all columns present in the original dataframe, but only those rows corresponding to the maximum matching.
import pandas as pd
from gurobi_optimods.bipartite_matching import maximum_bipartite_matching
# Read in some task-worker assignment data
frame = pd.DataFrame([
{"expert": "Jill", "task": "uphill"},
{"expert": "Jack", "task": "uphill"},
{"expert": "Jill", "task": "fetchpail"},
])
# Compute the maximum matching
matching = maximum_bipartite_matching(frame, "expert", "task")
The maximum_bipartite_matching function formulates a linear program for the
the network flow model corresponding to the given bipartite graph. Since the
model is formulated as a network flow, Gurobi will in most cases solve the model
using a network primal simplex algorithm.
Solution
The maximum matching is returned as a subgraph of the original bipartite
graph, as a scipy.sparse array. Inspecting the result, it is clear that
this is a maximum matching, since no two edges share a node in common, and
all nodes in the second set are incident to an edge in the matching.
>>> print(sp.triu(matching))
(0, 7) 1.0
(1, 6) 1.0
(3, 5) 1.0
The maximum matching is returned as a subgraph of the original bipartite
graph, as a nx.Graph graph. Inspecting the result, it is clear that
this is a maximum matching, since no two edges share a node in common, and
all nodes in the second set are incident to an edge in the matching.
import matplotlib.pyplot as plt
fig, (ax1, ax2) = plt.subplots(1, 2)
layout = nx.bipartite_layout(graph, nodes1)
nx.draw(graph, layout, ax=ax1)
nx.draw(matching, layout, ax=ax2)
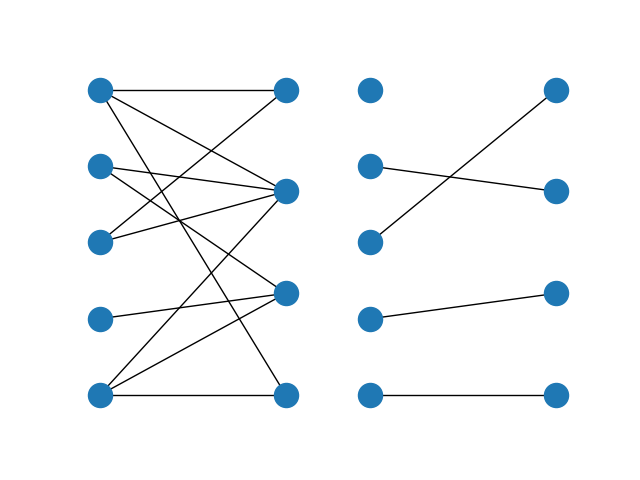
The maximum matching returns a subset of the original dataframe. We can see in this case that each expert is assigned exactly one task, and each task is only to be completed once.
>>> matching
expert task
0 Jack uphill
1 Jill fetchpail