Optimal Power Flow

The operation of power systems relies on a number of optimization tasks known as Optimal Power Flow (OPF) problems. The objective of a standard OPF problem is to minimize operational costs such that the underlying grid constraints on generation, demand, and voltage limits are satisfied.

This Mod considers the Alternating Current (AC) and Direct Current (DC) OPF formulations. The ACOPF problem, in its natural form, requires the introduction of complex numbers to formulate voltage constraints. This Mod uses a cartesian-coordinates formulation of ACOPF that reformulates complex-valued terms via nonconvex quadratic relationships. The DCOPF problem approximates the ACOPF problem by making additional assumptions to produce linear constraints. While the additional assumptions result in a potential loss of solution accuracy, they make the DCOPF problem much easier to solve. This is especially useful if the solution accuracy can be neglected in favour of solution time and problem size. Please refer to the Full Problem Specification for full details of the formulations.

Here we assume basic familiarity with concepts such as voltage (potential energy), current (charge flow), and power (instantaneous energy generation or consumption). The engineering community also uses the terms bus to refer to nodes in a network and branch to refer to arcs in a network (a connection between two buses, typically a line or a transformer). Please refer to the Recommended Literature section for more details and comprehensive descriptions of power systems and the underlying problems.

MATPOWER Case Input Format

This Mod has multiple API functions, each of which accepts a dictionary as input describing an OPF case. This case dictionary follows the MATPOWER Case Format conventions and holds all essential information about the underlying network: buses, branch connections, and generators. Several pre-defined MATPOWER cases can be loaded directly using the gurobi_optimods.datasets module. The following code loads an example case with 9 buses and displays the key fields:

baseMVA holds the base units of voltage for this case.

>>> from gurobi_optimods import datasets
>>>
>>> case = datasets.load_opf_example("case9")
>>> case['baseMVA']
100.0

Cases can also be read directly from MATPOWER format using read_case_matpower(). This function reads a standard MATLAB .mat data file holding the case data into the native Python format accepted by the Mod. For example:

case = opf.read_case_matpower("my_case.mat")

Solving an OPF Problem

After reading in or otherwise generating a MATPOWER case in the format described above, we can solve an OPF problem defined by the given network data. For this task, we use the solve_opf() function. We can define the type of the OPF problem that we want to solve by defining the opftype argument when calling the function. Currently, the available options are AC, ACrelax, and DC.

  • The AC setting solves an ACOPF problem defined by the given network data. The ACOPF problem is formulated as a nonconvex bilinear model as described in the ACOPF section of the Full Problem Specification. This setting yields the most accurate model of the physical power system. However, it is also the most difficult problem to solve and thus usually leads to the longer runtimes.

  • The AClocal setting solves the AC problem using adjusted settings to quickly find a good quality local solution, without attempting to solve to global optimality.

  • The ACrelax setting solves a Second Order Cone (SOC) relaxation of the nonconvex bilinear ACOPF problem formulation defined by the given network data. The relaxation is constructed by dropping nonconvex bilinear terms but simultaneously keeping the convex JABR inequalities, see JABR Relaxation for more details. This setting often yields a good approximation of the physical power system and is of moderate difficulty.

  • The DC setting solves a DCOPF problem defined by the given network data. The DCOPF problem is a linear approximation of the ACOPF problem, see DCOPF section of the Full Problem Specification for more details. This setting only yields a crude approximation of the physical power system, but is usually an easy problem that can be solved very quickly even for large networks.

The solve_opf function solves an AC problem unless the opftype argument specifies otherwise.

from gurobi_optimods import opf
from gurobi_optimods import datasets

case = datasets.load_opf_example("case9")
result = opf.solve_opf(case, opftype="AC")

...
Optimize a model with 19 rows, 107 columns and 28 nonzeros
...
Optimal solution found...
...
Objective value = 5296...
...

ACOPF and Branch Switching models are most often very hard to solve to optimality. For this reason, it is recommended to specify a solver time limit using the time_limit parameter. If the problem has not been solved to optimality within the time limit, the best known solution will be returned.

result = opf.solve_opf(case, opftype="AC", time_limit=60)

Solution Format

The Mod returns the result as a dictionary, following the same MATPOWER Case Format conventions as the case dictionary. However, in the result dictionary some object entries are modified compared to the input case dictionary. These modified fields hold the solution values of the optimization. There are also additional fields to store the solution information, as specified below.

The bus entries result['bus'][i]['Vm'] and result['bus'][i]['Va'] store the voltage magnitude (Vm) and voltage angle (Va) values in the OPF solution for bus i.

If a DCOPF problem was solved, additional fields result['bus'][i]['mu'] hold the shadow prices for balance constraints at bus i.

>>> result['bus'][0]
{... 'Vm': 1.09..., 'Va': 0.0, ...}

Plotting Feasible Solutions

In addition to solving an OPF problem, this Mod also provides plotting functions to display graphical representation of the network and the OPF result. There are already very involved graphical tools to represent OPF solutions provided by other packages such as:

thus the graphical representation provided by this Mod is kept intentionally simple. In order to use this functionality, it is necessary to install the plotly package as follows:

pip install plotly

In order to plot a previously obtained result, you must provide \((x, y)\) coordinates for all buses in the network. Coordinates are provided as a dictionary mapping bus IDs to coordinates. The OptiMods datasets module provides an example set of coordinates for plotting the 9 bus test case:

>>> coordinates = datasets.load_opf_extra("case9-coordinates")
>>> from pprint import pprint
>>> pprint(coordinates)
{1: (44.492, -73.208),
 2: (41.271, -73.953),
 3: (41.574, -73.966),
 4: (40.814, -72.94),
 5: (43.495, -76.451),
 6: (42.779, -78.427),
 7: (44.713, -73.456),
 8: (43.066, -76.214),
 9: (43.048, -78.854)}

Given a solution and a coordinate mapping, the plotting functions return plotly figures which can be displayed in a web browser. In the following code, we solve the DCOPF problem for a real-world dataset for the city of New York and produce a solution plot:

case = datasets.load_opf_example("caseNY")
solution = opf.solve_opf(case, opftype='DC')
coordinates = datasets.load_opf_extra("caseNY-coordinates")
fig = opf.solution_plot(case, coordinates, solution)
fig.show()  # open plot in a browser window
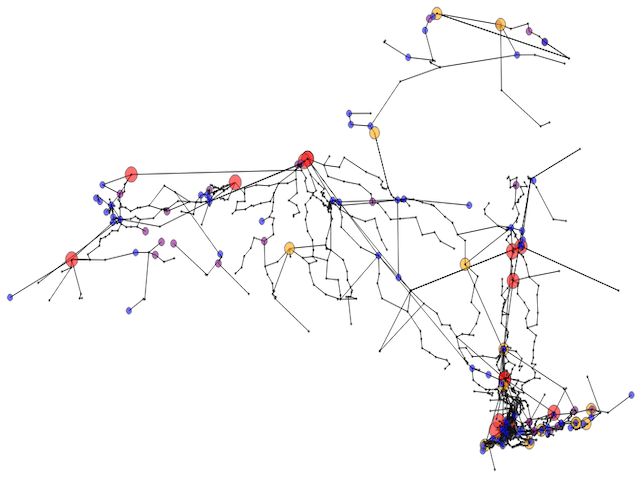
../../_images/opf.png

DCOPF solution for the New York power grid example dataset

The above image shows the grid solution generated from the given network data, plotted using the provided coordinates. The colored circles depict generators and the amount of power they generate:

  • Black bus: Power generation \(\leq 75\) and load \(< 50\)

  • Blue bus: Power generation \(\leq 75\) and load \(\geq 50\)

  • Purple bus: Power generation \(> 75\)

  • Orange bus: Power generation \(> 150\)

  • Red bus: Power generation \(> 500\)

Branch Switching

An important extension of the OPF problem is Branch Switching, where branches may be turned off. Note that already turning off a single branch changes the whole power flow through the network. Thus in practice, it is rare that branches are turned off at all, even if this option is enabled. If any are turned off, then it is usually only a small fraction of the overall power grid. For the mathematical formulation, please refer to the Branch Switching subsection of the Full Problem Specification.

To enable branch switching in a given OPF problem, set the branch_switching argument to True when calling gurobi_optimods.opf.solve_opf(). The Mod additionally offers the possibility to control the number of branches that must remain switched on via the min_active_branches argument. In practice, it is expected that only a very small fraction of branches are turned off. Thus, the default value of the min_active_branches argument is 0.9 (90%). In the following example, we solve a modified version of the 9 bus network to see whether branch switching allows a better solution.

case = datasets.load_opf_example("case9-switching")
result = opf.solve_opf(
    case, opftype="AC",
    branch_switching=True,
    min_active_branches=0.1,
    time_limit=60,
)

Plotting the resulting solution shows that one branch has been turned off in the optimal solution. Please note, that the used examplary network has been artificially adjusted to achieve this result and this is not the usual behavior in a realistic power grid of such small size.

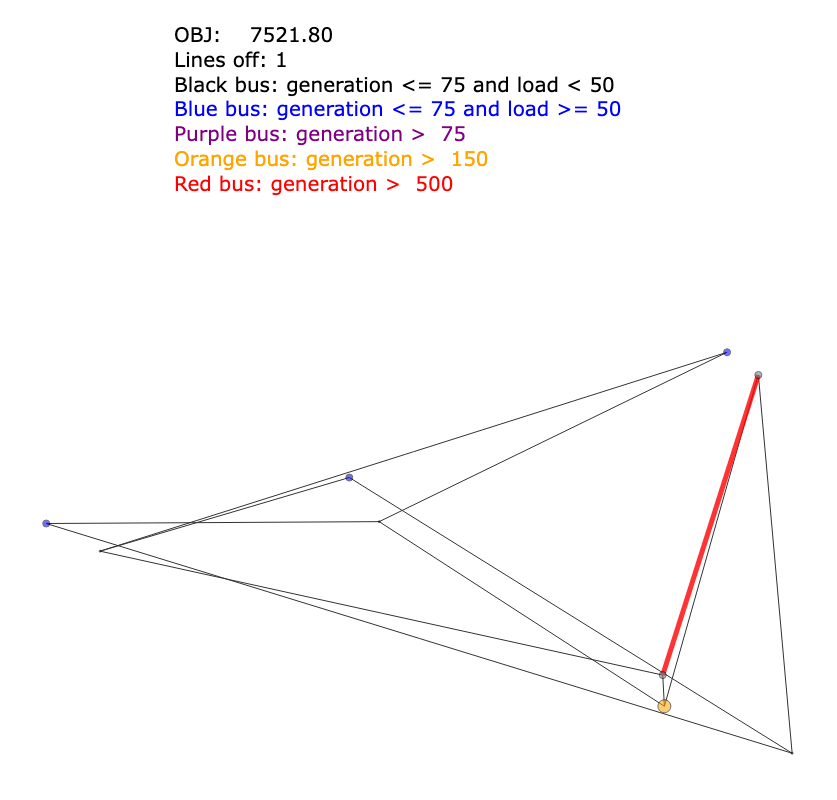
../../_images/switching_opf.png

Branch switching solution. The plot highlighted the switched-off branch in red

Violations for Pre-defined Voltage Values

In practice we may have voltage magnitudes and voltage angles for each bus at hand and would like to know whether these values are actually feasible within a given network. To tackle this problem, we can use the gurobi_optimods.opf.compute_violations() function. This function takes a set of bus voltages in addition to the case data and returns the computed violations in this voltage solution.

Bus voltages are provided as a dictionary mapping the Bus ID to a pair \((V_m, V_a)\) where \(V_m\) is the voltage magnitude and \(V_a\) is the voltage angle. An example is provided for the 9 bus case:

>>> voltages = datasets.load_opf_extra("case9-voltages")
>>> pprint(voltages)
{1: (1.089026, 0.0),
 2: (1.099999, 20.552543),
 3: (1.090717, 16.594399),
 4: (1.084884, -2.408447),
 5: (1.096711, 2.43001),
 6: (1.099999, 11.859651),
 7: (1.072964, 9.257936),
 8: (1.066651, 11.200108),
 9: (1.08914, 2.847507)}

Using this voltage data, we can check for possible model violations by calling the gurobi_optimods.opf.compute_violations() function. The function returns a dictionary which follows the MATPOWER Case Format with additional fields storing the violations for particular buses and branches.

The following fields in the violations dictionary are added to store violations data:

  • violation['bus'][i]['Vmviol'] Voltage magnitude violation at bus i

  • violation['bus'][i]['Pviol'] real power injection violation at bus i

  • violation['bus'][i]['Qviol'] reactive power injection violation at bus i

  • violation['branch'][i]['limitviol'] branch limit violation at branch i

volts_dict = datasets.load_opf_extra("case9-voltages")
case = datasets.load_opf_example("case9")
violations = opf.compute_violations(case, volts_dict)

>>> print(violations['branch'][6]['limitviol'])
66.33435...
>>> print(violations['bus'][3]['Pviol'])
-318.8997...

In this case, the limit at branch 6 and the real power injection at bus 3 are violated by the given input voltages.

Plotting Violations

Similar to generating a graphical representation of a feasible solution, it is also possible to generate a figure representing the violations within a given power grid. We can use the gurobi_optimods.opf.violation_plot() for this. The violations result is provided as input, along with the case and coordinate data, to produce this plot.

voltages = datasets.load_opf_extra("case9-voltages")
case = datasets.load_opf_example("case9")
coordinates = datasets.load_opf_extra("case9-coordinates")
violations = opf.compute_violations(case, voltages)
fig = opf.violation_plot(case, coordinates, violations)
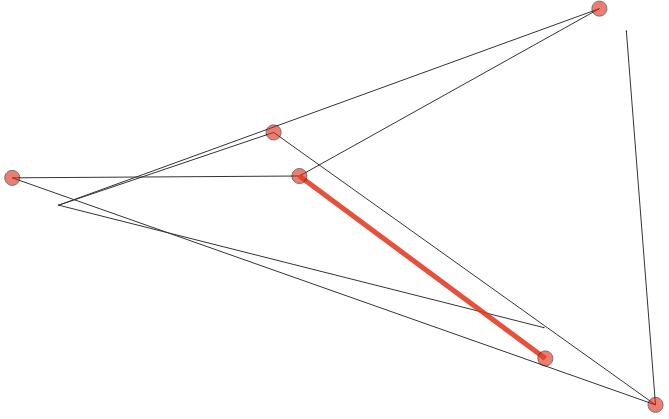
../../_images/violations_opf.png

The above image shows the power grid generated from the given network data together with coordinate and violation data. The red circles depict buses where the voltage magnitude or real or reactive power injections are violated. Red marked branches depict branches with violated limits.

Formulation Details

Full details of the formulations used in the OPF Mod are given in the following sections: